Compatible Numbers: Addition and Subtraction

The first time I taught students to use compatible numbers, I was totally unprepared.  I am guessing that my teachers did the same thing I did.  I read what the book said, followed its examples, and then told the kids to just round.  The next day we recycled their homework and moved on. EEK!

I saw the light after attending a workshop with Greg Tang. It transformed my teaching and how I help my students think about numbers. The goal is to see familiar facts within a given problem and make use of them.

Successfully using compatible numbers requires two things:
1. Make 10 Fact Fluency: Students need to quickly recognize ways to make ten/tens with the numbers in the problem. A few minutes a day investing in practicing these 11 facts makes a huge impact on lots of math skills. Click here to download a poster

2. Ability to Decompose Numbers: Understanding that numbers are flexible and how to apply Addition and Multiplication Properties is essential.  When students do not understand that they can break numbers apart to make them easier to work with, they will not understand how to use compatible numbers to their advantage.

Check this out:


I could add these using a standard algorithm, but students are likely to make simple errors trying to keep track of all of those steps.  It would be a lot easier for me to add 36 + 44 (see the Make 10 fact 6+4?)  How do I make that happen?  By breaking apart my numbers.



By taking away 1 from 45 I am left with two numbers that are easy for me to add in my head. BTW-You could have just as easily taken 1 away from 36 to add 35 + 45. The facts most familiar to the person solving it will be the ones that they see.


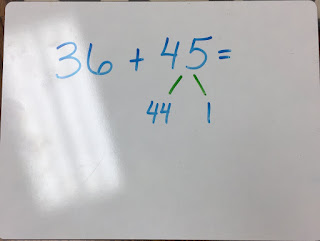
If I want an estimate, this is where I would complete my problem.

If I am looking for an exact answer, I would add the 1 that I took away when making my compatible numbers.

This is very similar to the Near Doubles addition strategy that students learn. They only have to fluently learn a small number of facts, then they are able to use those with strategy to add a large set of facts. Revisit Near Doubles strategies to scaffold using compatible numbers with multi-digit addition and subtraction.



Awesome Resources:
Whack a Number: Addition with Compatible Numbers without Regrouping

Whack a Number: Addition with Compatible Numbers with Regrouping

Whack a Number: Subtraction with Compatible Numbers without Regrouping

Whack a Number: Subtraction with Compatible Numbers with Regrouping

Greg Tang Math Break Apart

Greg Tang Math Printables